Imagine searching for “best restaurants in Paris” and getting a list of places with “best” and “Paris” in their name — rather than actual top-rated restaurants. Frustrating, right? Traditional keyword search works like this: it looks for exact matches rather than understanding what you really mean.
This is where vector search changes the game.
Instead of just matching words, vector search understands concepts — grasping the meaning behind your query, even if the exact keywords aren’t there. It’s the difference between a search engine that acts like an index and one that acts like a smart assistant that truly gets what you’re looking for.
At its core, vector search transforms words into numbers (vectors), allowing it to measure relationships between concepts. This enables businesses to deliver highly relevant search results, improve recommendation engines, and create more intuitive digital experiences.
So, how does vector search work? And why does it matter for enterprises drowning in unstructured data? Let’s break it down.
Vectors Are a Math Thing (But Let’s Keep It Simple)
At its core, vector search turns words into numbers — but not just any numbers. These numbers, called vectors, represent meaning in a way that allows a computer to compare how similar two concepts are.
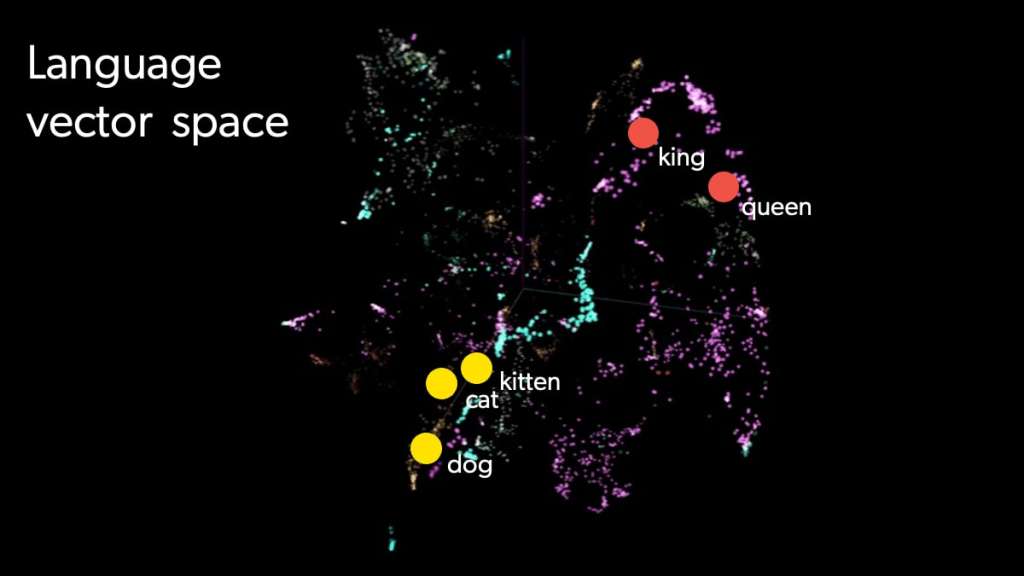
Think of a vector as a pinpoint on a multi-dimensional map. Instead of mapping locations, it maps ideas. Words and phrases that are closely related — like “laptop” and “notebook” — will be positioned near each other in this space. Meanwhile, unrelated words — like “laptop” and “banana” — will be farther apart.
To understand this, let’s start with something familiar: a basic graph with an X and Y axis.
- If you’ve ever plotted points on a graph, you’ve used a 2D vector — it has two numbers (coordinates) that define its position.
- Add another dimension, and you get 3D vectors — which help define things in physical space, like latitude, longitude, and altitude.
Now, imagine hundreds or thousands of dimensions—this is how computers represent the complex relationships between words, concepts, and ideas in a vector search engine. While we can’t visualize these high-dimensional spaces, the principle remains the same: closer = more similar, farther = less similar.
This mathematical approach allows search engines to understand meaning beyond exact keywords, making results more relevant and intuitive. Now, let’s see how it works in action.
How Does Vector Search Work?
So how does vector search actually work under the hood? It relies on machine learning algorithms, particularly Approximate Nearest Neighbor (ANN), to map and retrieve related concepts efficiently. This is why vector search is faster than most other kinds of search. What makes vector search powerful is that we can turn up related concepts, not just keywords in an end user’s search result.
Information retrieval has long relied on keyword search, which looks for a word or phrase in a document as well as how often it appears in that document. It can’t match synonyms, understand sentence meaning, know the intent behind a query, or help with search relevance.
Fortunately, search has matured in the last 50 years to give us more relevant results that focus on user intent. Vector search is at the heart of that because we can ask a question in a conversational way and get relevant answers, fast. In an enterprise setting, combining traditional keyword matching with vector search and AI allows for precise, efficient retrieval of information from large datasets.
For example, if you search for ‘wireless headphones’ on an e-commerce site, vector search groups related products (e.g., ‘Bluetooth earbuds’) even if they don’t contain the exact keywords.
Let’s break it down.
What Is A Vector Representation?
In a nutshell, vector search uses a procedure called embedding to turn words into lists of numbers (vectors) to measure vector similarity, or how similar those words are. The outputs of the process are called word embeddings, or also sometimes called a vector representation. These live in a vector space (a collection of vectors).
(In practice, “embeddings” gets used as shorthand to refer to both the mapping process and the end result, which can be a bit semantically confusing.)
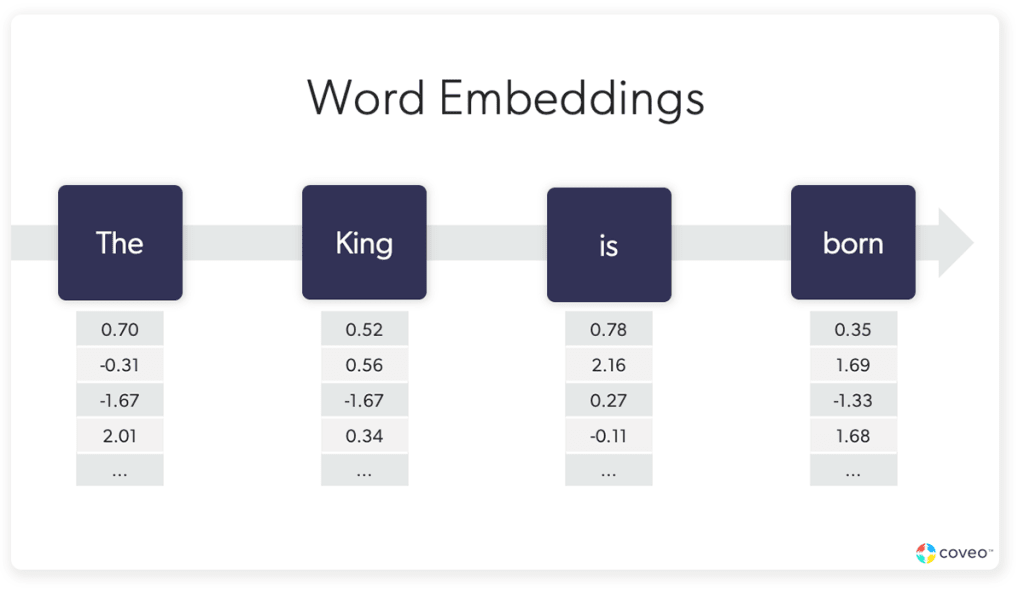
This little workhorse is at the heart of other techniques that you hear more about, including semantic search, natural language processing, generative AI, and similarity search.
There are different technical variations in the exact way that vector search works, but the basic idea centers on the concept of ANN algorithm search in a vector space.
Measuring Vector Similarity
So vectors allow us to turn unstructured data into numeric representations, and that data includes words, images, queries, and even products. Data and its vectors sync up through similarity – and show results that match searchers’ questions and intent.
We use similarity metrics to match data to queries. And this is where wading through the above paragraphs about lines, graphs, and vector space comes in.
When we talk about how related two pieces of unstructured data are, we need some way to measure the distance between them in the vector space. Vectors measure similarity (Remember the café and restaurant question above?) with angles. This means that the direction of the vector, rather than the length of the vector, is important. The direction of the lines determines the width of the angle, which is how we measure similarity.
Looking at our graph again, we see three vectors.
- Vector A is 2,1.
- Vector B is 3.2.
- Vector C is -1, 2.
The angle between vector A and vector B is much smaller than the angle between Vector A and Vector C.
Narrow angles tell us that things are closely related, even if one line segment is much longer than another. Again, we’re interested in the direction of the vector, not the length.
If there is 180-degree angle between two vectors, it tells you that they are anti-related, which can be valuable information. If the angle is 90 degrees, these two vectors have nothing to tell you about one another.
Measuring the similarity or distance between two vectors is called a cosine distance, because the actual computation of the distance (a number) uses the cosine function.
Look at a map of Manhattan and you’ll see that most of the streets run up-down (north/south) and left-right (east/west). When we need to see how far the best bagel store is from our hotel, someone will tell us that it’s three blocks up and one block down.
This is one way to measure distance — how far the bagel shop is from where I am (the origin) is called the Manhattan distance. But there’s also distance as the crow flies, which is a different measurement called Euclidean distance. There are many ways to measure distance, but these two examples give us the idea.
In vector search, closer means “more related” and further means “less related.”
How Does a Vector Search Engine Work?
There are a number of ways to calculate similarity in vector search. A simple cosine similarity match (looking at the angles between vectors) is called a naïve approach by technologists. It works, but it’s slow.
Other approaches use various types of indexing to speed up information retrieval. Thinking of indexing in terms of books is helpful. A geometry book might have an index of topics in the back. You would look for the word “vector”, find the page it was on, and flip to that page. It’s a lot faster than skimming the book to find information you need.
Indexing over a large document set achieves the same thing – you have a list of concepts and where you can find those concepts in your documents. This process creates a vector index. When someone conducts a query, you can now quickly find the information that matches the query.
Vector search has several types of indexing, including the Nearest Neighbor Index (NNI) , which is a type of similarity search. NNIs group similar vectors together and create short paths to vectors that are not similar. If we return to our book example, a NNI is kind of like a “see also” note in an index. If we look at our map of Manhattan, an NNI would group neighborhoods together and show you how they’re connected — Chinatown is nearer to Tribeca and farther from the Upper East Side.
In vector search, similarity is gauged by angles, whereas indexing makes finding that similarity easier by grouping vectors that are alike and creating paths between those that are alike and those that aren’t.
The result is that every vector in the index is connected to several other vectors in a structure that keeps the most similar vectors near to one another but ensures that even far away vectors have relatively short paths connecting them.
Why Vector Search Matters for Enterprises — And Its Limitations
Enterprises are drowning in unstructured data — emails, support tickets, knowledge bases, product catalogs, internal documents, and customer interactions. Traditional keyword search struggles with this sheer volume, often returning incomplete or irrelevant results because it relies on exact word matches rather than understanding meaning.
Vector search expands enterprise search capabilities by analyzing intent and context, making it possible to surface the most relevant information, even when queries are vague or phrased differently. This is a breakthrough for enterprises that need to:
- Improve Customer Support – Help users find the right answers instantly, reducing agent workload and improving self-service.
- Boost Employee Productivity – Enable teams to quickly locate internal documents, reducing time wasted searching for critical information.
- Power Smarter E-Commerce Experiences – Deliver personalized product recommendations based on meaning, not just keywords.
- Strengthen Security & Compliance – Retrieve the right documents while respecting permissions and access controls.
Limitations of Vector Search
Despite its advantages, vector search isn’t perfect. Like many AI-driven technologies, it comes with challenges:
- Lack of Transparency: Unlike keyword search, where results are easy to trace, vector search works in high-dimensional spaces, making it harder to explain why certain results appear.
- Task-Specific Performance: Embeddings work best in environments they are trained for. A vector model optimized for customer support won’t necessarily work well for e-commerce recommendations.
- Computational Complexity: Searching across thousands or millions of dense vector representations requires significant processing power, especially compared to traditional keyword search.
Because of these limitations, the future of search lies in hybrid search—a combination of vector search, keyword-based (lexical) search, and AI-powered techniques.
The Future: Hybrid Search
Hybrid search leverages the best of both worlds — the precision and familiarity of keyword search, combined with the intelligence and flexibility of vector search. It integrates machine learning, natural language processing, and large language models (LLMs) to provide fast, accurate, and context-aware search results.
In fact, hybrid search is already evolving to include generative AI and conversational interfaces, allowing users to engage with search in a natural, question-answer format.
Understanding vector search lays the foundation for embracing hybrid search — the next step in delivering powerful, enterprise-ready search experiences.
As AI-driven search evolves, enterprises will need hybrid search to stay competitive. The future isn’t just about retrieving data — it’s about understanding user intent, predicting needs, and delivering hyper-relevant experiences.
Ready to outpace the competition with industry-leading hybrid search? Contact an AI search expert at Coveo today.


